Mario writes,
I wanted to ask you if among all those great blog-tutorials of yours, there is simple ball-to-ball collision resonse tutorial. Like billiard kind of 2D physics? I need it for a game Im working on that needs collision response between circular asteroids. (including mass)If not, would you please consider writing one?
There probably is, but it’ll be buried somewhere on the blitzbasic.com forums. So, here’s a new one!
The key insight for ball-to-ball collisions is that, at the moment of impact, the distance between the two balls is the sum of their radii, and the repulsive force is applied along the line between their centres. I’m going to use a lot of vector maths here, because it makes the maths a lot clearer.
So, the first task to detect a collision is to get the distance between the centres of the two balls. If the distance is less than their radii added together, then the balls have collided.
I’ll build up what needs to happen next through a few example cases. I’m not going to really explain the mechanics in depth because there’s loads of messy algebra and I have better things to do, but this should give you the idea.
Case 1: Ball 1 is stationary, ball 2 is travelling directly at ball 1, both balls have the same mass.
When the balls collide, the total momentum needs to be preserved, and the forces applied to each ball need to be of the same size. I’ll also assume the collision is elastic, so the total kinetic energy of the system stays the same. The only solution is that all of ball 2’s momentum is transferred to ball 1. Ball 2 stops and ball 1 starts moving in the same direction and at the same speed as ball 2.
Case 2: Ball 1 is stationary, ball 2 is travelling directly at ball 2, different masses.
One of Newton’s laws of motion is that force is equal to mass times acceleration:
As the forces applied to each ball need to be equal, it follows that if the balls have different masses, the heavier ball accelerates less than the lighter one. In fact, the acceleration of ball 1 is proportional to
This way, the momentum is conserved:
Case 3: Both balls moving, ball 2 is travelling directly at ball 1, equal masses.
When both balls are moving, you can make the calculation simpler by considering only the relative velocities of the balls. By subtracting ball 1’s velocity from ball 2’s, you can perform the calculation as if ball 1 is stationary, and the resulting force will be the same.
Case 4: Ball 1 stationary, ball 2 hits ball 1 at an angle, equal masses.
The force is applied along the line between the two balls, so when that line isn’t parallel to the relative velocity, the balls bounce off each other at an angle.
All those cases put together should be enough to solve collisions in general. Here’s some code:
Global gwidth=800,gheight=600
Global balls:TList=New TList
Type ball
Field x#,y# 'position
Field vx#,vy# 'velocity
Field radius#
Field mass#
Method New()
balls.addlast Self
End Method
Function Create:ball(x#,y#,radius#,mass#)
b:ball=New ball
b.x=x
b.y=y
b.radius=radius
b.mass=mass
b.vx=(gwidth/2-x)*.01
b.vy=(gheight/2-y)*.01
Return b
End Function
Method update()
x:+vx
y:+vy
'wrap edges of screen around
If x<0
x:+gwidth
EndIf
If x>gwidth
x:-gwidth
EndIf
If y<0
y:+gheight
EndIf
If y>gheight
y:-gheight
EndIf
End Method
Function collideAll()
l:TList=balls.Copy()
While l.Count()>1
b:ball=ball(l.removefirst())
For b2:ball=EachIn l
dx#=b2.x-b.x 'get relative positions of b2 with respect to b
dy#=b2.y-b.y
d#=Sqr(dx*dx+dy*dy) 'get square of distance between b and b2
dd#=b.radius+b2.radius-d 'get amount balls overlap
If dd>0 'if distance between balls is less than their radii added together, then they are overlapping
dx:/d 'by dividing the difference between the two balls' positions, we get a unit vector pointing from b to b2
dy:/d
dvx#=b2.vx-b.vx 'get relative velocity of b2 with respect to b
dvy#=b2.vy-b.vy
f#=dvx*dx+dvy*dy 'calculate force of impact - project relative velocity vector onto line from b to b2
f:*2/(b.mass+b2.mass)
b2.vx:-dx*f*b.mass 'push b2 away from b
b2.vy:-dy*f*b.mass
b.vx:+dx*f*b2.mass 'push b in the opposite direction
b.vy:+dy*f*b2.mass
b.x:-dd*dx*b2.mass/(b.mass+b2.mass) 'position the balls so they are just touching and no longer overlap
b.y:-dd*dy*b2.mass/(b.mass+b2.mass)
b2.x:+dd*dx*b.mass/(b.mass+b2.mass)
b2.y:+dd*dy*b.mass/(b.mass+b2.mass)
EndIf
Next
Wend
End Function
Method draw()
shade#=mass*5
SetColor shade,shade,shade
DrawOval x-radius,y-radius,radius*2,radius*2
'because the edges of the screen wrap round, draw again shifted by a screen's width/height to maintain the illusion
DrawOval gwidth+x-radius,y-radius,radius*2,radius*2
DrawOval x-radius,gheight+y-radius,radius*2,radius*2
DrawOval -gwidth+x-radius,y-radius,radius*2,radius*2
DrawOval x-radius,-gheight+y-radius,radius*2,radius*2
End Method
End Type
Function changeState()
balls=New TList
state=(state+1) Mod 5
Select state
Case 0
b1:ball=ball.Create(400,300,50,50)
b1.vx=0
b1.vy=0
b2:ball=ball.Create(200,300,50,50)
b2.vx=1
b2.vy=0
Case 1
b1:ball=ball.Create(400,300,50,50)
b1.vx=0
b1.vy=0
b2:ball=ball.Create(200,300,20,20)
b2.vx=1
b2.vy=0
Case 2
b1:ball=ball.Create(400,300,50,50)
b1.vx=1
b1.vy=0
b2:ball=ball.Create(200,300,50,50)
b2.vx=2
b2.vy=0
b3:ball=ball.Create(400,450,50,50)
b3.vx=0
b3.vy=0
b4:ball=ball.Create(200,450,50,50)
b4.vx=1
b4.vy=0
Case 3
b1:ball=ball.Create(400,300,50,50)
b1.vx=-1
b1.vy=0
b2:ball=ball.Create(200,250,50,50)
b2.vx=1
b2.vy=0
Case 4
For c=1 To 5
radius#=Rnd(10,50)
mass=Rnd(.5,1)*radius
ball.Create Rand(radius,gwidth-radius),Rand(radius,gheight-radius),radius,mass
Next
End Select
End Function
Function drawlines(txt$,x,y)
Local lines$[]=txt.split("~n")
For i=0 To Len(lines)-1
DrawText lines[i],0,y
y:+13
Next
End Function
Graphics gwidth,gheight,0
SeedRnd MilliSecs()
Global state=-1
Global statetxt$[]=[ "Ball 1 stationary~nBall 2 heading directly at ball 1~nEqual masses",..
"Ball 1 stationary~nBall 2 heading directly at ball 1~nDifferent masses",..
"Both balls moving~nBall 2 heading directly at ball 1~nEqual masses~nBall 1's frame of reference shown below",..
"Ball 1 stationary~nBall 2 hits ball 1 at an angle~nEqual masses",..
"Lots of balls all over the place!"]
changeState
While Not (KeyHit(KEY_ESCAPE) Or AppTerminate())
If KeyHit(KEY_SPACE)
changeState
EndIf
ball.collideAll
For b:ball=EachIn balls
b.update
Next
For b:ball=EachIn balls
b.draw
Next
SetColor 255,255,255
Drawlines statetxt[state],0,0
Flip
Cls
Wend
and 
are the horizontal and vertical radii.
from the vertical to the edge of the ellipse. Call the length 
, so the co-ordinates of the end are given by
out:
is distance travelled, 
is initial velocity, 
is acceleration, and 
is time elapsed.
and the end point at 
.
, the distance to the end point is 
, and the height of the wall is 
.
and the angle it is fired at is 
in terms of 
to get
to get
:
to shoot the projectile at which will satisfy this equation.
. Use the 
is the component of the vector which is perpendicular to the wall. If 
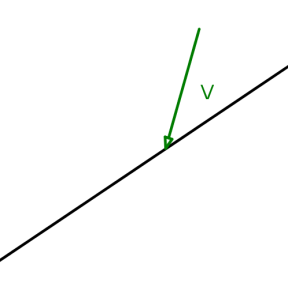
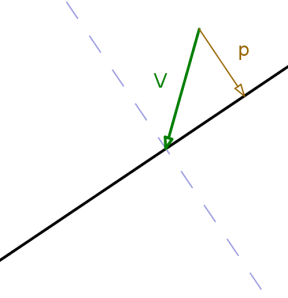
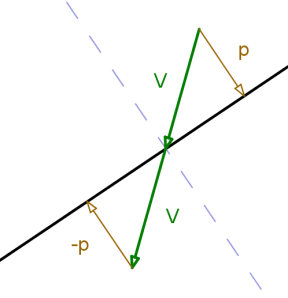
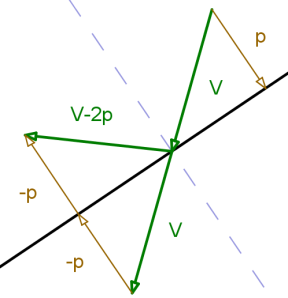So that’s the theory – we need to work out 
.
and 
. 
, and an enemy at initial position 
moving in the direction 
.
.
and 
, then the bullet will move in parallel with the enemy, always staying the same distance from it.
. The bullet can move along this line to collide with the bullet.
![\begin{array}{rcl} \left(\frac{1}{t}\right)^2 \left[ (x_1 - x_0)^2 + (y_1 - y_0)^2 \right] && \\ + \frac{1}{t} \left[ v_x (x_1 - x_0) + v_y ( y_1 - y_0) \right] &&\\ + v_x^2 + v_y^2 - V^2 &=& 0 \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D+%5Cleft%28%5Cfrac%7B1%7D%7Bt%7D%5Cright%29%5E2+%5Cleft%5B+%28x_1+-+x_0%29%5E2+%2B+%28y_1+-+y_0%29%5E2+%5Cright%5D+%26%26+%5C%5C+%2B+%5Cfrac%7B1%7D%7Bt%7D+%5Cleft%5B+v_x+%28x_1+-+x_0%29+%2B+v_y+%28+y_1+-+y_0%29+%5Cright%5D+%26%26%5C%5C+%2B+v_x%5E2+%2B+v_y%5E2+-+V%5E2+%26%3D%26+0+%5Cend%7Barray%7D&bg=ffffff&fg=333333&s=0&c=20201002)
![\begin{array}{rcl} a &=& (x_1-x_0)^2 + (y_1-y_0)^2 \\ b &=& 2[ v_x(x_1-x_0) + v_y(y_1-y_0) ] \\ c &=& v_x^2 + v_y^2 - V^2 \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D+a+%26%3D%26+%28x_1-x_0%29%5E2+%2B+%28y_1-y_0%29%5E2+%5C%5C+b+%26%3D%26++2%5B+v_x%28x_1-x_0%29+%2B+v_y%28y_1-y_0%29+%5D+%5C%5C+c+%26%3D%26++v_x%5E2+%2B+v_y%5E2+-+V%5E2+%5Cend%7Barray%7D&bg=ffffff&fg=333333&s=0&c=20201002)
and 
, and you’re done!
Warpy Code Maths Blog 