Making things bounce

Local vx#,vy# ‘V, the velocity of the object before it hits the wall

Local wallangle# ‘the angle of the wall

‘now work out the normal vector to the wall – it’s just at right angles

Local nx#,ny#

nx = Cos(wallangle + 90)

ny = Sin(wallangle + 90)

‘p is the projection of V onto the normal

Local px#,py#

Local dotproduct# = vx*nx+vy*ny

px = dotproduct*nx

py = dotproduct*ny

‘the velocity after hitting the wall is V – 2p, so just subtract 2*p from V

vx = vx – 2*px

vy = vx – 2*py

‘done!

Andres asked in this post:

i’m having problems with a formula for my early stage game.

i want to calculate how the object bounces (the angle) from the wall.

i know the angle of the wall, object’s moving angle, the point where object and wall collide. If possible then the function or formula would work if the object comes from the other side of the wall too.

Countless other people have asked this as well. It’s one of those things that comes up very often but is quite tricky to work out for yourself.

So, to start with, we’ve got something hitting a wall. We know its velocity before it hits the wall and we want to know what its velocity becomes after it hits the wall.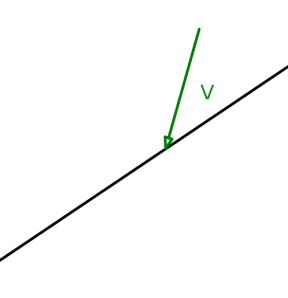 

When an object bounces off a wall, it travels at the same angle from the wall as it went in at, but the other way round. I stated that in terms of angles, but that’s tricky to get into code because, while people always know to write an angle as 90° anti-clockwise instead of 270° clockwise, and how to do stuff like reflections properly, it isn’t so simple when you’re just dealing with numbers in a computer. For this example, there are four choices of escape angle that you could produce if you’re not careful, but it’s hard to say which one is the correct one.

So instead, consider as a cartesian vector – that is, an x-component and a y-component. We could also think of it as having a component moving parallel to the wall, and one moving perpendicular to it.

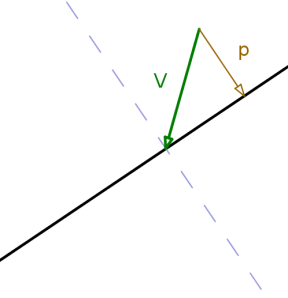
In the above image, is the component of the vector which is perpendicular to the wall. If didn’t bounce off the wall but instead kept travelling as it was before, travelling backwards along from the end of would get you back on the line:

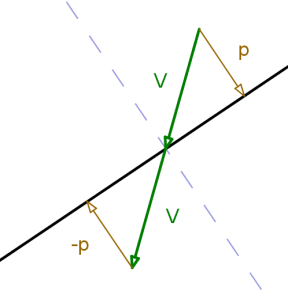
And if you move back in the direction of one more time, you’ll end up pointing exactly where you want to be: the angle of escape is the same as the angle of entry.

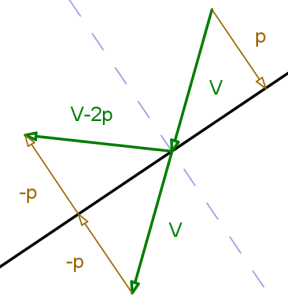So that’s the theory – we need to work out and , and the object’s velocity after hitting the wall will be .

is easy – you might already have it in vector form, or if not, you can use and . is the projection of onto the wall’s normal vector. (I’m planning on writing a post about the various vector operations later, but this one takes just a couple of lines of code to work out and considerably more writing to explain, so I won’t.)

And the great thing about this method is that you don’t need to check which side of the wall the object is hitting, or which way round the normal is pointing – it all works out correctly anyway.

Local vx#,vy#		'V, the velocity of the object before it hits the wall
Local wallangle#	'the angle of the wall

'now work out the normal vector to the wall - it's just at right angles
Local nx#,ny#
nx = Cos(wallangle + 90)
ny = Sin(wallangle + 90)

'p is the projection of V onto the normal
Local px#,py#
Local dotproduct# = vx*nx+vy*ny
px = dotproduct*nx
py = dotproduct*ny

'the velocity after hitting the wall is V - 2p, so just subtract 2*p from V
vx = vx - 2*px
vy = vx - 2*py

'done!

I hope that was helpful.

Read Full Post »

A triangle puzzle

Jussi writes,

Given the lengths of c1 and c2 and angle alpha, what’s the simplest and fastest way to calculate the length of d (see the attached image)?

Looks tricky at first, but trying to do it the boring way ended up giving me a nice answer.

What we want is to have the line with angle alpha intersect the hypotenuse of the triangle. So, let’s write down the equations of the two lines:

The hypotenuse can be written using the normal straight line formula:

While the other line is in polar co-ordinates because we only know the angle alpha:

Substitute those into the first equation:

We want to find d, so collect all the terms with d together:

And finally divide by the stuff in the brackets:

Now let’s check that it works with some bmax code:

Graphics 600,600,0

c1#=300
c2#=400

an#=0

While Not (KeyHit(KEY_ESCAPE) Or AppTerminate())
	x#=300-c2/2
	y#=300-c1/2
	DrawLine x,y,x+c2,y
	DrawLine x,y,x,y+c1
	DrawLine x+c2,y,x,y+c1

	an = (an+1) Mod 90

	t#=an/90
	r#=c1/(Sin(an)+(c1/c2)*Cos(an))
	DrawLine x,y,x+Cos(an)*r,y+Sin(an)*r

	Flip
	Cls
Wend

Yep!

Read Full Post »

Aiming accurately at moving targets

In this post, SpaceTW asked:

Hi, I need help aiming at moving targets for a program. I have the variables for the speed and direction of the enemies, but the targeting is still not accurate enough.

There’s a very simple solution if you don’t mind the bullets travelling at different speeds, but that can lead to bullets travelling very fast or very slow, so let’s say that we want every bullet to go the same speed. Here’s the solution:

Suppose you have a tower at a fixed position , and an enemy at initial position moving in the direction .

You want to shoot a bullet travelling at a certain velocity so that it collides with the enemy.

Let the direction of the bullet be .

If and , then the bullet will move in parallel with the enemy, always staying the same distance from it.

You can now consider that the enemy is not moving at all, relative to the bullet, and the difference in position between them is . The bullet can move along this line to collide with the bullet.

If the bullet takes frames to reach the bullet, we now get:

As we said that the bullet’s velocity is , we get

Which expands out to:

(I had to split that over a few lines so it would fit in the post column, sorry!)

Which is a quadratic equation! So set:

Then, using the quadratic formula:

You can now put that back into the equations for and , and you’re done!

Here’s the result, written in BlitzMax:

diffx:double=x2-x1
diffy:double=y2-y1
v:Double=3                'desired speed of bullet

a:Double=diffx*diffx+diffy*diffy
b:Double=2*(vx*diffx+vy*diffy)
c:Double=vx*vx+vy*vy-v*v

tInv#=(-b+Sqr(b*b-4*a*c))/(2*a)   ' solve 1/t
dx=diffx*tInv+vx
dy=diffy*tInv+vy

That’s it!

Read Full Post »

Finding the intersection of a line and a box

In this post Ryan Burnside asked how to find the exact place where a line intersects the outline of a box.

Here’s my solution:

Function boxintersect(last_x#, last_y#, x#, y#, bx1#, by1#, bx2#, by2#, ix# Var, iy# Var)
	'finds point of intersection of line from (last_x,last_y) to (x,y)
	'with the box (bx1,by1,bx2,by2). the ix and iy parameters are var pointers, which means
	'the function fills in the values of the point of intersection in the variables that you give.
	'the function also returns true if there is an intersection, and false if there is none.

	If Not (x>=bx1 And x=by1 And y<=by2) Return False

	If last_x = bx1 		'does it cross left edge?
		iy# = last_y + (y - last_y) * (bx1-last_x)/(x-last_x)
		If iy>=by1 And iy bx2 And x =by1 And iy<=by2			'is intersection point on right edge?
			ix# = bx2
			Return True
		EndIf
	EndIf

	If last_y = by1 		'does it cross top edge?
		ix# = last_x + (x - last_x) * (by1 - last_y)/(y - last_y)
		If ix>=bx1 And ix by2 And y =bx1 And ix<=bx2			'is intersection point on bottom edge?
			iy# = by2
			Return True
		EndIf
	EndIf
End Function

'example
Graphics 800,600,0

Global box1#,boy1#,box2#,boy2#
Global ox#,oy#,nx#,ny#

Function maketest()
	box1=Rnd(200,300)
	boy1=Rnd(100,200)
	box2=Rnd(500,600)
	boy2=Rnd(400,500)

	nx=Rnd(box1,box2)
	ny=Rnd(boy1,boy2)
	an#=Rnd(360)
	ox=300*Cos(an)+400
	oy=300*Sin(an)+300

End Function

maketest

While Not (KeyHit(KEY_ESCAPE) Or AppTerminate())

	If KeyHit(KEY_SPACE)
		'make a new box and line
		maketest
	EndIf

	DrawLine box1,boy1,box2,boy1
	DrawLine box1,boy1,box1,boy2
	DrawLine box1,boy2,box2,boy2
	DrawLine box2,boy1,box2,boy2

	DrawLine ox,oy,nx,ny

	Local ix#,iy#	'variables to store point of intersection in
	boxintersect( ox,oy,nx,ny, box1,boy1,box2,boy2, ix,iy )

	DrawOval ix-3,iy-3,6,6

	Flip
	Cls
Wend

The way it works is to notice that one line crosses another if it starts on one side of the crossed line, and ends on the other. That’s what the first check is about, checking the infinite line which the side of the box is part of. The second check finds the intersection point and checks if it is actually within the line segment which makes up the box.

Read Full Post »